Питання 1: 4D Сонце

Уявіть, що вас перенесли в інший всесвіт із чотирма просторовими вимірами. Яким буде колір Сонця в цьому чотиривимірному всесвіті? Ви можете припустити, що температура поверхні Сонця така ж, як у нашому Всесвіті, і становить приблизно T  = 6 × 10 ³  К.

Стала Больцмана, k _B  = 1,38 × 10 ⁻²³  Дж K ⁻¹
Швидкість світла, c  = 3 × 10 ⁸  м с ⁻¹

Питання 2: Heavy stuff

У паралельному Всесвіті дві точкові маси, кожна по 1 kg, знаходяться у стані спокою на відстані 1 m одна від одної. Єдина сила, що на них діє – сила гравітаційного притяжіння F = –Gm₁m₂/r². Якщо для їх зустрічі посередині потрібно 26  годин і 42 хвилини, підрахуйте значення гравітаційної сталої G у цьому Всесвіті.

Question 4: Quantum stick

Imagine an infinitely thin stick of length 1 m and mass 1 kg that is balanced on its end. Classically this is an unstable equilibrium, although the stick will stay there forever if it is perfectly balanced. However, in quantum mechanics there is no such thing as perfectly balanced due to the uncertainty principle – you cannot have the stick perfectly upright and not moving at the same time. One could argue that the quantum mechanical effects of the uncertainty principle on the system are overpowered by others, such as air molecules and photons hitting it or the thermal excitation of the stick. Therefore, to investigate we would need ideal conditions such as a dark vacuum, and cooling to a few milli­kelvins, so the stick is in its ground state.

Moment of inertia for a rod,

I=13ml2I=13ml2

where m is the mass and l is the length.

Uncertainty principle,

ΔxΔp≥ℏ2ΔxΔp≥ℏ2

There are several possible approximations and simplifications you could make in solving this problem, including:

sinθ ≈ θ for small θ

cosh−1x=ln (x+√x2−1)cosh−1x=ln x+x2−1

and

sinh−1x=ln (x+√x2+1)sinh−1x=ln x+x2+1

Calculate the maximum time it would take such a stick to fall over and hit the ground if it is placed in a state compatible with the uncertainty principle. Assume that you are on the Earth’s surface. [10 marks]

Question 3: Just like clockwork

Consider a pendulum clock that is accurate on the Earth’s surface. Figure 1 shows a simplified view of this mechanism.

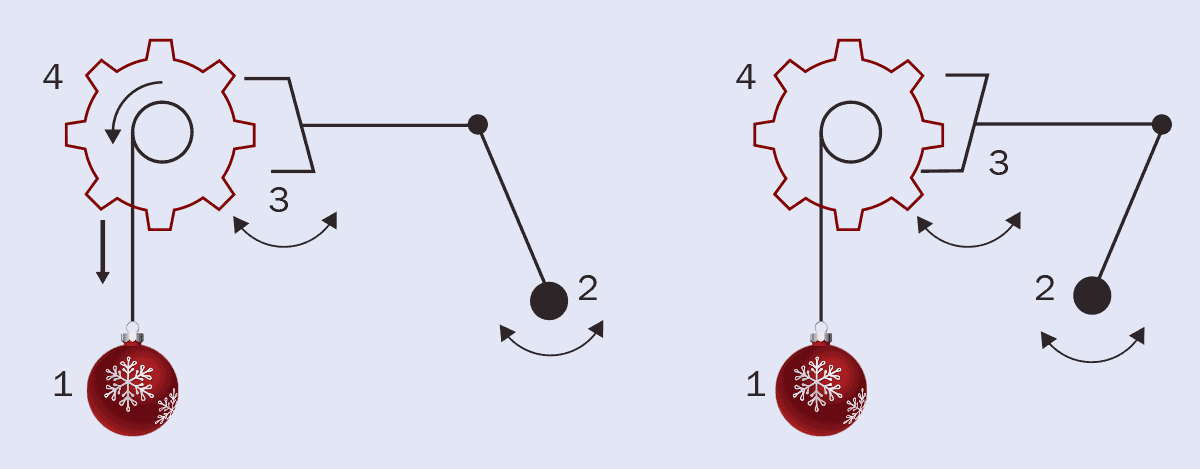
A pendulum clock runs on the gravitational potential energy from a hanging mass (1). The other components of the clock mechanism regulate the speed at which the mass falls so that it releases its gravitational potential energy over the course of a day. This is achieved using a swinging pendulum of length l (2), whose period is given by

T=2π√lgT=2πlg

where g is the acceleration due to gravity.

Each time the pendulum swings, it rocks a mechanism called an “escapement” (3). When the escapement moves, the gear attached to the mass (4) is released. The mass falls freely until the pendulum swings back and the escapement catches the gear again. The motion of the falling mass transfers energy to the escapement, which gives a “kick” to the pendulum that keeps it moving throughout the day.

Radius of the Earth, R = 6.3781 × 10⁶ m

Period of one Earth day, τ₀ = 8.64 × 10⁴ s

How slow will the clock be over the course of a day if it is lifted to the hundredth floor of a skyscraper? Assume the height of each storey is 3 m.